Lab 4: Exploratory Data Analysis

The goal of this lab is to acquire skills in running descriptive statistics and creating graphs using R. Make sure you’ve read and fully understood Handout 4 as this guide tracks closely with the material presented there. In this lab, we will be working with census tract data from the U.S. American Community Survey and the U.S. Department of Agriculture. As described in Handout 3, census tracts are the traditional measure of neighborhoods in the United States. The objectives of the guide are as follows

Learn how to use various R functions to summarize neighborhood characteristics
Learn how to make presentation-ready tables of descriptive statistics
Introduction to R graphics

This lab guide follows closely and supplements the material presented in Chapters 1,3, 7 and 28 in the textbook R for Data Science (RDS) and the class Handout 4.

Assignment 4 is due by 12:00 pm, April 30th on Canvas. See here for assignment guidelines. You must submit an .Rmd file and its associated .html file. Name the files: yourLastName_firstInitial_asgn04. For example: brazil_n_asgn04.

Open up a R Markdown file

Download the Lab template into an appropriate folder on your hard drive (preferably, a folder named ‘Lab 4’), open it in R Studio, and type and run your code there. The template is also located on Canvas under Files. Change the title (“Lab 4”) and insert your name and date. Don’t change anything else inside the YAML (the stuff at the top in between the ---). Also keep the grey chunk after the YAML. For a rundown on the use of R Markdown, see the assignment guidelines

Installing and loading packages

We will be installing two new packages in this lab. Install the following packages. These packages will be needed to create presentation ready tables. Remember, you only do this once, and never within your R Markdown.

install.packages("flextable")
install.packages("webshot")

Load the following packages using library(). Remember, you need to do this every time you run an R session, so the following code should appear at the top of your R Markdown file.

library(tidyverse)
library(flextable)
library(webshot)

Reading in census tract data

You will be working with census tract data for the counties of Sacramento, San Diego, Santa Clara, and Fresno, four of the largest counties in California. To save us time, I downloaded Census data, wrangled the data, and uploaded it on GitHub. The data file and its metadata are also located on Canvas in the Week 4 Lab folder under Files. Let’s bring the csv file into R using read_csv().

cal.tracts <- read_csv("https://raw.githubusercontent.com/crd150/data/refs/heads/master/lab4_data.csv")

Make sure you take a look at any dataset you bring into R.

glimpse(cal.tracts)

## Rows: 1,514
## Columns: 7
## $ GEOID     <dbl> 6085507904, 6085508504, 6085508505, 6085508704, 6085509403, …
## $ county    <chr> "Santa Clara County", "Santa Clara County", "Santa Clara Cou…
## $ medincome <dbl> 206607, 114300, 152969, 145500, 112278, 210529, 250001, 1360…
## $ phisp     <dbl> 0.03286385, 0.15841469, 0.08540341, 0.19652036, 0.34261983, …
## $ pblk      <dbl> 0.0000000000, 0.0103440260, 0.0000000000, 0.0399367339, 0.02…
## $ mhisp     <chr> "Not Majority", "Not Majority", "Not Majority", "Not Majorit…
## $ status    <chr> "Urban", "Urban", "Urban", "Urban", "Urban", "Urban", "Urban…

The dataset contains tract-level median household income, percent Hispanic, percent Black, whether the tract is urban, suburban or rural according to Rural-Urban Commuting Area Codes (RUCA) and whether the tract is “Majority” Hispanic (phisp > 50%) or “Not Majority” Hispanic.

Summarizing a single variable

Recall from Handout 4 our two important data types: categorical and numeric. Let’s first summarize a single numeric variable - neighborhood median household income - using some basic descriptive statistics.

Numeric variables

We can use the function summarize() to calculate mean neighborhood income. The first argument inside summarize() is the data object cal.tracts and the second argument is the function calculating the specific summary statistic, in this case mean(), which unsurprisingly calculates the mean of the variable you indicate in between the parentheses.

cal.tracts %>%
      summarize(mean(medincome))

## # A tibble: 1 × 1
##   `mean(medincome)`
##               <dbl>
## 1                NA

We get the value NA, which as we learned in Lab 3 represents a missing value. If a variable has missing values, functions like mean() will return an NA. If we use the function summary(), we find that medincome has 6 tracts with missing median income values

summary(cal.tracts)

##      GEOID              county            medincome          phisp       
##  Min.   :6.019e+09   Length:1514        Min.   : 12417   Min.   :0.0000  
##  1st Qu.:6.067e+09   Class :character   1st Qu.: 56479   1st Qu.:0.1512  
##  Median :6.073e+09   Mode  :character   Median : 82443   Median :0.2475  
##  Mean   :6.068e+09                      Mean   : 88873   Mean   :0.3181  
##  3rd Qu.:6.073e+09                      3rd Qu.:112372   3rd Qu.:0.4360  
##  Max.   :6.086e+09                      Max.   :250001   Max.   :0.9864  
##                                         NA's   :6                        
##       pblk            mhisp              status         
##  Min.   :0.00000   Length:1514        Length:1514       
##  1st Qu.:0.01092   Class :character   Class :character  
##  Median :0.02974   Mode  :character   Mode  :character  
##  Mean   :0.04994                                        
##  3rd Qu.:0.06997                                        
##  Max.   :0.40050                                        
##

In order to calculate the mean (or any numeric descriptive statistic) for a variable with missing values, use the argument na.rm = TRUE, which will calculate the mean of the variable without the missing values.

summarize(cal.tracts, mean(medincome, na.rm = TRUE))

## # A tibble: 1 × 1
##   `mean(medincome, na.rm = TRUE)`
##                             <dbl>
## 1                          88873.

Does the average neighborhood income differ by county? We need to pair summarize() with the function group_by() to answer this question. The function group_by() tells R to run subsequent functions on the data object by a group characteristic (such as gender, educational attainment, or in this case, county). Let’s use our new best friend %>%, who we met in Lab 2, to accomplish this task.

cal.tracts %>%
  group_by(county) %>%
  summarize(mean(medincome, na.rm = TRUE))

## # A tibble: 4 × 2
##   county             `mean(medincome, na.rm = TRUE)`
##   <chr>                                        <dbl>
## 1 Fresno County                               57128.
## 2 Sacramento County                           71183.
## 3 San Diego County                            83753.
## 4 Santa Clara County                         129391.

The first pipe sends cal.tracts into the function group_by(), which tells R to group cal.tracts by the variable county.

cal.tracts %>%
  group_by(county)

How do you know the tibble is grouped? Because it tells you

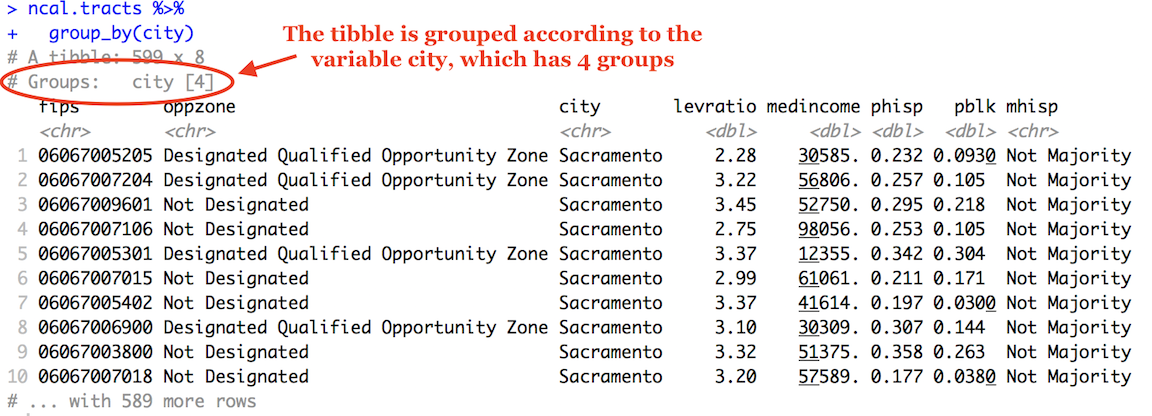
The second pipe takes this grouped dataset and sends it into the summarize() command, which calculates the mean neighborhood income (by county, because the dataset is grouped by county).

We can calculate more than one summary statistic within summarize(). For example, to get the mean, median, standard deviation and interquartile range (IQR) of median income, and give column labels for the variables in the resulting summary table, we type in

cal.tracts %>%
  group_by(county) %>%
  summarize(Mean = mean(medincome,  na.rm = TRUE),
            Median = median(medincome, na.rm = TRUE),
            SD = sd(medincome,  na.rm = TRUE),
            IQR = IQR(medincome,  na.rm = TRUE))

## # A tibble: 4 × 5
##   county                Mean Median     SD    IQR
##   <chr>                <dbl>  <dbl>  <dbl>  <dbl>
## 1 Fresno County       57128.  50318 28347. 36875.
## 2 Sacramento County   71183.  65114 29249. 37807 
## 3 San Diego County    83753.  79953 33262. 42475 
## 4 Santa Clara County 129391. 123469 46599. 60069.

Remember from Handout 4 that the IQR is the difference between the 75th and 25th percentiles. It is a measure of spread, and more generally, an indicator of inequality. Another measure of spread or inequality is the 90/10 ratio. To calculate this ratio, we’ll first need to calculate the 90th and 10th percentiles using the quantile() command, where we indicate the percentile using the argument p =. We can do all of this inside summarize(). Make sure you understand what each function in the code below is doing, and what the values reported are showing.

cal.tracts %>%
  group_by(county) %>%
  summarize(p90 = quantile(medincome, p = 0.90,  na.rm = TRUE),
            p10 = quantile(medincome, p = 0.10,  na.rm = TRUE),
            Ratio9010 = p90/p10) %>%
  select(-(c(p90,p10)))

## # A tibble: 4 × 2
##   county             Ratio9010
##   <chr>                  <dbl>
## 1 Fresno County           3.57
## 2 Sacramento County       2.89
## 3 San Diego County        2.80
## 4 Santa Clara County      2.58

Categorical variables

Let’s next summarize a single categorical variable. status indicates whether a tract is urban, suburban or rural.

To get the proportion of tracts that are urban, suburban and rural, you’ll need to combine the functions group_by(), summarize() and mutate() using %>%.

cal.tracts %>%
  group_by(status) %>%
  summarize(n = n()) %>%
  mutate(total = sum(n),
        freq = n / total)

## # A tibble: 3 × 4
##   status       n total   freq
##   <chr>    <int> <int>  <dbl>
## 1 Rural       20  1514 0.0132
## 2 Suburban    86  1514 0.0568
## 3 Urban     1408  1514 0.930

Let’s break up this chunk of code to show exactly what was done here. First, cal.tracts was piped into the group_by() function. Next, group_by(status) separates the neighborhoods by geographic status. We then used summarize() to count the number of neighborhoods by geographic status. The function to get a count is n(), and we saved this count in a variable named n. This gave us the following table.

cal.tracts %>%
  group_by(status) %>%
  summarize (n = n())

## # A tibble: 3 × 2
##   status       n
##   <chr>    <int>
## 1 Rural       20
## 2 Suburban    86
## 3 Urban     1408

Remember, we are trying to get the proportion of neighborhoods that are urban, suburban and rural. This means we need a numerator - the number of neighborhoods that are urban, suburban and rural. This is what n = n() gives us. There are 1,408 neighborhoods that are designated as urban.

Next, this table is piped into mutate(), which creates a variable total which gives you the denominator - the total number of neighborhoods. The code sum(n) adds the values of n: 1408+86+20 = 1514. We then create a variable freq, which divides the value of each n by this sum: 20/1514. = 0.0132, 86/1514 = 0.0568 and 1408/1514. = 0.930. This yields the proportion of all neighborhoods by geographic status (how would you transform this to a percentage?).

cal.tracts %>%
  group_by(status) %>%
  summarize (n = n()) %>%
    mutate(total = sum(n),
        freq = n / total)

## # A tibble: 3 × 4
##   status       n total   freq
##   <chr>    <int> <int>  <dbl>
## 1 Rural       20  1514 0.0132
## 2 Suburban    86  1514 0.0568
## 3 Urban     1408  1514 0.930

Summarizing two variables

The functions we’ve gone through so far describe one variable. It is often the case that we are interested in understanding whether two variables are associated with one another.

Let’s go through the ways we can describe the association between: (1) two categorical variables; (2) one categorical variable and one numeric variable; and (3) two numeric variables.

Two categorical variables

To summarize the relationship between two categorical variables, you’ll need to find the proportion of observations for each combination, also known as a cross tabulation. Let’s create a cross tabulation of the categorical variables status and mhisp. We do this by using both variables in the group_by() command.

cal.tracts %>%
  group_by(status, mhisp) %>%
  summarize(n = n())  %>%
    mutate(total = sum(n),
        freq = n / total)

## # A tibble: 6 × 5
## # Groups:   status [3]
##   status   mhisp            n total  freq
##   <chr>    <chr>        <int> <int> <dbl>
## 1 Rural    Majority        14    20 0.7  
## 2 Rural    Not Majority     6    20 0.3  
## 3 Suburban Majority        35    86 0.407
## 4 Suburban Not Majority    51    86 0.593
## 5 Urban    Majority       264  1408 0.188
## 6 Urban    Not Majority  1144  1408 0.812

A much higher proportion of rural neighborhoods are Majority Hispanic (0.7) compared to urban neighborhoods (0.188).

One categorical, one numeric

A typical way of summarizing the relationship between a categorical variable and a numeric variable is to take the mean of the numeric variable for each level of the categorical variable. We can get the mean median household income for urban, suburban and rural neighborhoods using the following code.

cal.tracts %>%
  group_by(status) %>%
  summarize("Mean Income" = mean(medincome, na.rm = TRUE))

## # A tibble: 3 × 2
##   status   `Mean Income`
##   <chr>            <dbl>
## 1 Rural           46034.
## 2 Suburban        81730.
## 3 Urban           89891.

Let’s separate by county by adding county to the group_by() function.

cal.tracts %>%
  group_by(county, status) %>%
  summarize("Mean Income" = mean(medincome, na.rm = TRUE))

## # A tibble: 12 × 3
## # Groups:   county [4]
##    county             status   `Mean Income`
##    <chr>              <chr>            <dbl>
##  1 Fresno County      Rural           41470.
##  2 Fresno County      Suburban        56237 
##  3 Fresno County      Urban           58808.
##  4 Sacramento County  Rural           40395 
##  5 Sacramento County  Suburban        87334.
##  6 Sacramento County  Urban           70536.
##  7 San Diego County   Rural           51555.
##  8 San Diego County   Suburban        91427.
##  9 San Diego County   Urban           83710.
## 10 Santa Clara County Rural           99000 
## 11 Santa Clara County Suburban       113092.
## 12 Santa Clara County Urban          130456.

Which counties have the biggest differences income between rural and urban neighborhoods?

Two numeric variables

You can summarize the relationship between two numeric variables with the correlation coefficient. To calculate the correlation coefficient, use the function cor(). The first two arguments in cor() are the two numeric variables you want to calculate the correlation for. Let’s calculate the correlation between neighborhood income and percent black. Note that the argument use = "complete.obs" removes the missing values in medincome.

cal.tracts %>%
  summarize(blk_inc = cor(medincome,pblk, use = "complete.obs"))

## # A tibble: 1 × 1
##   blk_inc
##     <dbl>
## 1  -0.398

Group these correlations by county

cal.tracts %>%
  group_by(county) %>%
  summarize(blk_inc = cor(medincome,pblk, use = "complete.obs"))

## # A tibble: 4 × 2
##   county             blk_inc
##   <chr>                <dbl>
## 1 Fresno County       -0.337
## 2 Sacramento County   -0.449
## 3 San Diego County    -0.338
## 4 Santa Clara County  -0.305

Make sure you understand what these values mean (see Handout 4).

Tables for presentation

The output from the descriptive statistics we’ve ran so far is not presentation ready. For example, taking a screenshot of the following results table produces unnecessary information that is confusing and messy.

cal.tracts %>%
  group_by(county) %>%
  summarize(Mean = mean(medincome,  na.rm = TRUE),
            Median = median(medincome, na.rm = TRUE),
            SD = sd(medincome,  na.rm = TRUE),
            IQR = IQR(medincome,  na.rm = TRUE))

## # A tibble: 4 × 5
##   county                Mean Median     SD    IQR
##   <chr>                <dbl>  <dbl>  <dbl>  <dbl>
## 1 Fresno County       57128.  50318 28347. 36875.
## 2 Sacramento County   71183.  65114 29249. 37807 
## 3 San Diego County    83753.  79953 33262. 42475 
## 4 Santa Clara County 129391. 123469 46599. 60069.

Furthermore, you would like to show a table, say, in your final project that does not require you to take a screenshot, but instead can be produced via code, that way it can be fixed if there is an issue, and is reproducible.

One way of producing presentation tables in R is through the flextable package. First, before creating any table, run the following code to ensure that the tables you save will have a transparent or white background (the default is gray).

set_flextable_defaults(background.color = "white")

Next, you will need to save the tibble or data frame of results into an object. For example, let’s save the above results into an object named cal.summary

cal.summary <- cal.tracts %>%
  group_by(county) %>%
  summarize(Mean = mean(medincome,  na.rm = TRUE),
            Median = median(medincome, na.rm = TRUE),
            SD = sd(medincome,  na.rm = TRUE),
            IQR = IQR(medincome,  na.rm = TRUE))

You then input the object into the function flextable(). Save it into an object called my_table

my_table <- flextable(cal.summary)

If you type in my_table in the console, you should see a relatively clean table pop up in the Viewer window. We can progressively pipe the my_table object through flextable formatting functions. For example, you can change the column header names using the function set_header_labels() and center the header names using the function align()

my_table <- my_table %>%
          set_header_labels(
            county = "County",
            Mean = "Mean",
            Median = "Median",
            SD = "Standard Deviation",
            IQR = "IQR") %>%
  colformat_double(digits = 1) %>%
  align(align = "center")

my_table

County	Mean	Median	Standard Deviation	IQR
Fresno County	57,127.6	50,318.0	28,346.9	36,874.8
Sacramento County	71,183.0	65,114.0	29,248.9	37,807.0
San Diego County	83,753.0	79,953.0	33,261.5	42,475.0
Santa Clara County	129,391.5	123,469.0	46,599.2	60,068.8

There are a slew of options for formatting your table, including adding footnotes, borders, shade and other features. Check out this useful tutorial for an explanation of some of these features.

Once you’re done formatting your table, you can then export it to Word, PowerPoint or HTML or as an image (PNG) files. To do this, use one of the following functions: save_as_docx(), save_as_pptx(), save_as_image(), and save_as_html(). For the final project, you will likely be saving your tables as images. Before saving, make sure your working directory is set to the appropriate folder (use getwd() to get the current working directory). Then use the save_as_image() function

save_as_image(my_table, path = "cal_income.png")

You first put in the table my_table, and set the file name with the png extension. Check your working directory on your hard drive. You should see the file cal_income.png in the folder.

Summarizing variables using graphs

Another way of summarizing variables and their relationships is through graphs and charts. The main package for R graphing is ggplot2 which is a part of the tidyverse package. The graphing function is ggplot() and it takes on the basic template

ggplot(data = <DATA>) +
      <GEOM_FUNCTION>(aes(x, y)) +
      <OPTIONS>()

ggplot() is the base function where you specify your dataset using the data = <DATA> argument.
You then need to build on this base by using the plus operator + and <GEOM_FUNCTION>() where <GEOM_FUNCTION>() is a unique geom function indicating the type of graph you want to plot. Each unique function has its unique set of arguments which you specify using the aes() argument. aes() stands for aesthetics - things we can see. Within aes() you specify the variables you need to plot in the given geom() or graph, typically based on what is plotted on the x = and y = axes. Charts and graphs have an x-axis, y-axis, or both. Check this ggplot cheat sheet for all possible geoms.
<OPTIONS>() are a set of functions you can specify to change the look of the graph, for example relabelling the axes or adding a title.

The basic idea is that a ggplot graphic layers geometric objects (circles, lines, etc), themes, and scales on top of data.

You first start out with the base layer. It represents the empty ggplot layer defined by the ggplot() function with the data object whose variable(s) you want to graph.

ggplot(cal.tracts)

We get an empty plot. We haven’t told ggplot() what type of geometric object(s) we want to plot, nor how the variables should be mapped to the geometric objects, so we just have a blank plot. We need geoms to paint the blank canvas.

From here, we add a geom layer to the ggplot object. Layers are added to ggplot objects using +, instead of %>%, since you are not explicitly piping an object into each subsequent layer, but adding layers on top of one another. Each geom is associated with a specific type of graph. For example, below is code that creates a histogram

ggplot(cal.tracts) + 
  geom_histogram(aes(x=medincome))

cal.tracts is <DATA>, geom_histogram() is the <GEOM_FUNCTION>(), and x=medincome is the variable in cal.tracts we are graphing. There is no y argument specified because a histogram only plots one variable (just on the x axis). Let’s go through how to create the graphs outlined in Handout 4.

Bar charts

Recall from Handout 4 that we use bar charts to summarize categorical variables. Bar charts, also known as bar plots, show either the number or frequency of each category. To create a bar chart, use geom_bar() for <GEOM_FUNCTION>(). Let’s show a bar chart of status. We can use a bar chart to show the number or count of observations for each category.

ggplot(cal.tracts) +
    geom_bar(aes(x=status))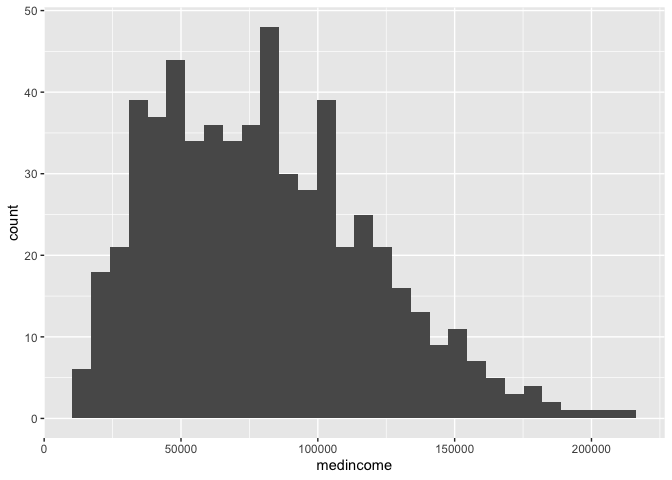

What if instead of counts, we want to show the proportions of each category? ggplot() can’t automatically do this for us, so we have to calculate those proportions (or percentages) on our own. We can borrow from the code we used earlier to create our status frequency table and pipe this table directly into ggplot().

cal.tracts %>% 
  group_by(status) %>%
  summarize (n = n()) %>%
    mutate(total = sum(n),
        freq = n / total)  %>%
  ggplot() +
    geom_bar(aes(x=status, y=freq),
             stat="identity")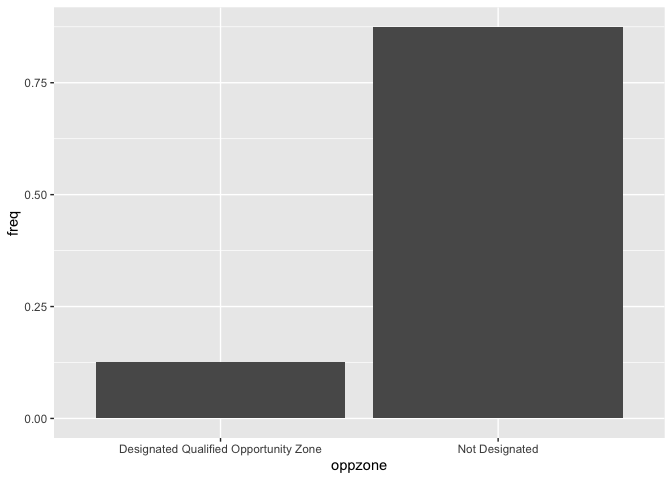

We didn’t need to specify data = <DATA> in ggplot() because it was piped in. Within aes(), we specified the categorical variable status on the x-axis and then the proportion of neighborhoods freq on the y-axis. The argument stat = "identity" tells ggplot() to plot the exact value listed for the variable freq. Why is this outside the aes() function? Variables (or columns of your data set) have to be defined inside aes(). Whereas to apply a modification on everything, we can set an aesthetic to a constant value outside of aes(). Type ? geom_bar() to see what other arguments you can use outside of the aes() argument.

The X and Y axes labels are not so great. Interpretable labels are important for getting your message across clearly. We can relabel the axes using the xlab() and ylab() functions, which are examples of <OPTIONS>() functions.

cal.tracts %>% 
  group_by(status) %>%
  summarize (n = n()) %>%
    mutate(total = sum(n),
        freq = n / total) %>%
  ggplot() +
    geom_bar(aes(x=status, y=freq),
             stat="identity") +
    xlab("Geographic Status") +
    ylab("Proportion")

Histograms

Histograms are used to summarize a single numeric variable. To create a histogram, use geom_histogram() for <GEOM_FUNCTION()>. Let’s create a histogram of median household income with an clearly defined axis label.

ggplot(cal.tracts) + 
  geom_histogram(aes(x=medincome)) +
  xlab("Median Household Income")

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

## Warning: Removed 6 rows containing non-finite outside the scale range
## (`stat_bin()`).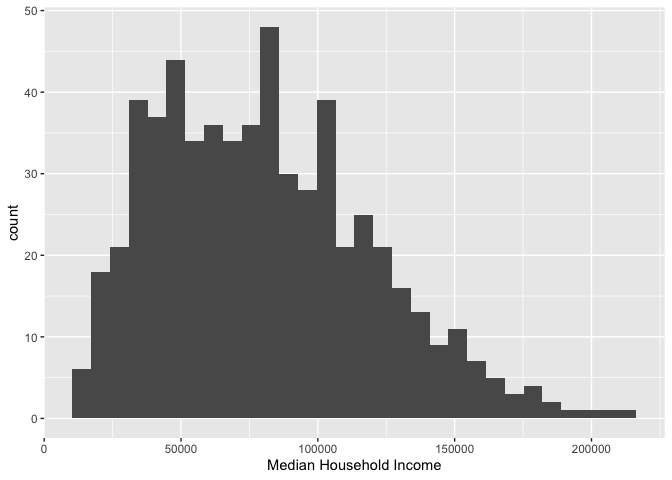

As described earlier, because a single variable is plotted on the x-axis, we specify x = in aes() but not a y =. The message before the plot tells us that we can use the bins = argument to change the number of bins used to produce the histogram. You can increase the number of bins to make the bins narrower and thus get a finer grain of detail. Or you can decrease the number of bins to get a broader visual summary of the shape of the variable’s distribution. Try changing the number of bins and see what you get.

Boxplots

We can use a boxplot to visually summarize the distribution of a single variable or the relationship between a categorical and numeric variable. Use geom_boxplot() for <GEOM_FUNCTION()> to create a boxplot. Let’s examine median household income.

ggplot(cal.tracts) +
     geom_boxplot(aes(y = medincome))+
    ylab("Median Household Income")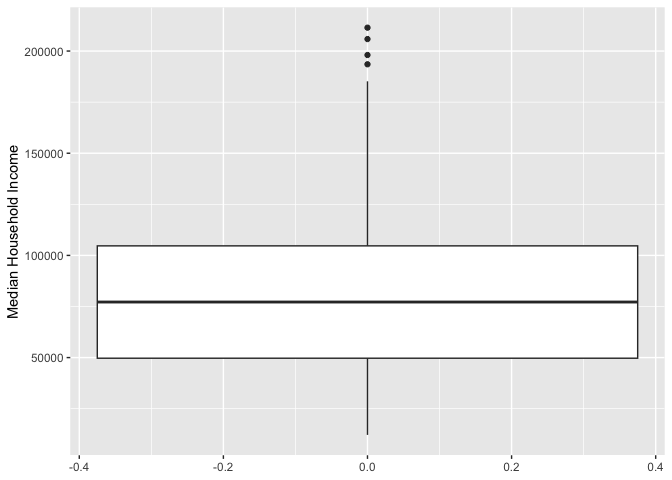

Remember from Handout 4 that the points outside the whiskers represent outliers. Outliers are defined as having values that are either larger than the 75th percentile plus 1.5 times the IQR or smaller than the 25th percentile minus 1.5 times the IQR. The IQR is $55,893, the 75th percentile is $112,372 and the 25th percentile is $56,479. While we don’t see outliers at the bottom, we do see outliers at the top - these are neighborhoods with median income values greater than $112,372 + 1.5*$55,893 = $196,211.5.

Let’s examine the distribution of median income by urban, suburban and rural. Because we are examining the association between two variables, we need to specify x and y variables within aes().

ggplot(cal.tracts) +
    geom_boxplot(aes(x = status, y = medincome)) +
    xlab("Geographic Status") +
    ylab("Median Household Income")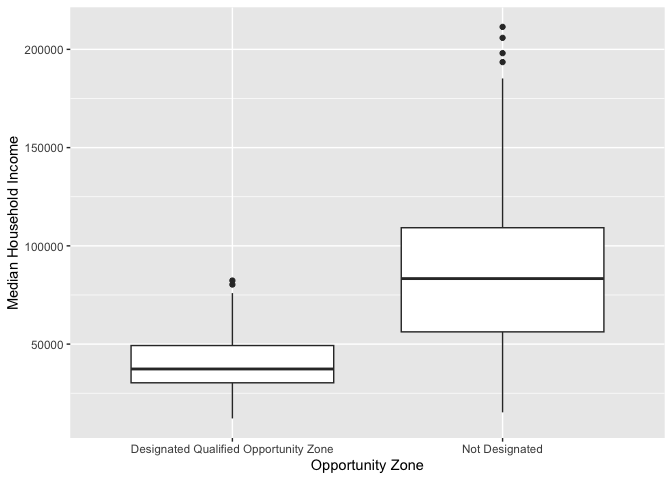

The boxplot is for all neighborhoods combined. We can use the facet_wrap()function to separate by county.

ggplot(cal.tracts) +
  geom_boxplot(aes(x = status, y = medincome)) +
  xlab("Geographic Status") +
  ylab("Median Household Income") +
  facet_wrap(~county)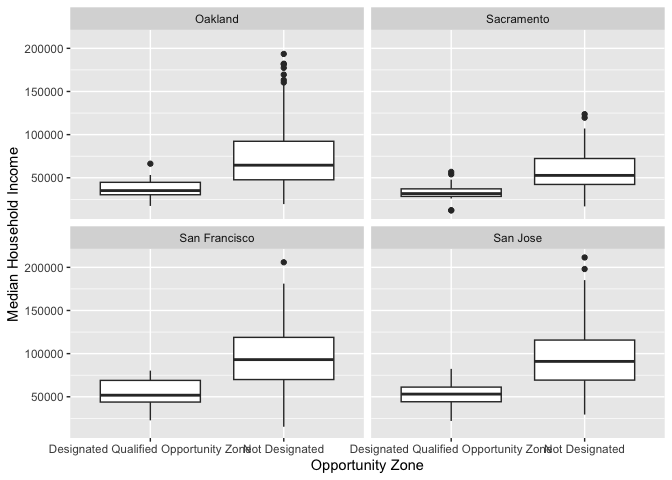

Note the tilde operator ~ before county

We can flip the axes and can create horizontal boxplots. To create horizontal boxplots, add the coord_flip() function at the end.

ggplot(cal.tracts) +
    geom_boxplot(aes(x = status, y = medincome)) +
    facet_wrap(~county) +
    ylab("Median Household Income") +
    xlab("Geographic Status") +
    coord_flip()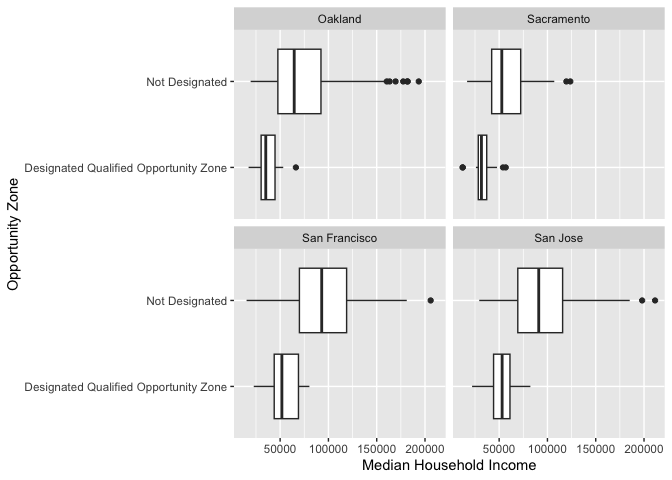

Scatterplots

The scatterplot is the traditional graph for visualizing the association between two numeric variables. For scatterplots, we use geom_point() for <GEOM_FUNCTION>(). Because we are plotting two variables, we specify an x and y variable. Does median household income change with greater percent Hispanic in the neighborhood?

ggplot(cal.tracts) +
    geom_point(aes(x = phisp, y = medincome)) +
    xlab("Percent Hispanic") +
    ylab("Median Household Income")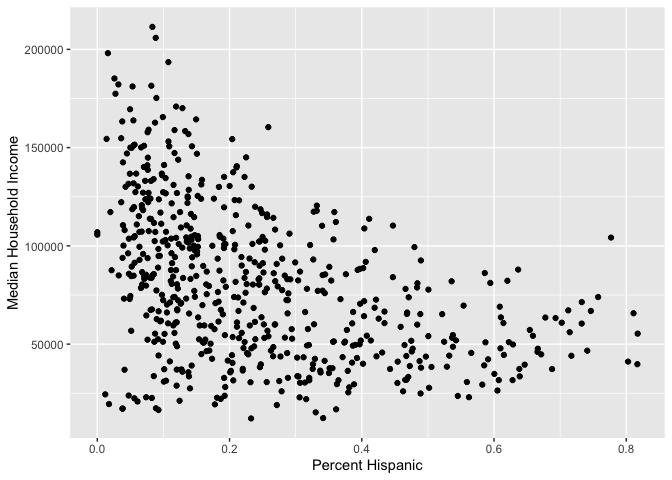

And for each county?

ggplot(cal.tracts) +
    geom_point(aes(x = phisp, y = medincome)) +
    xlab("Percent Hispanic") +
    ylab("Median Household Income") +
    facet_wrap(~county)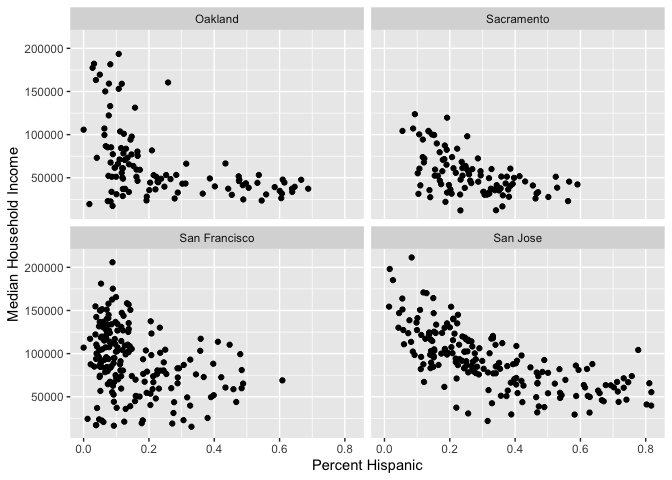

What do these scatter plots suggest about the relationship between income and percent Hispanic across these four counties?

ggplot() is a powerful function, and you can make a lot of visually captivating graphs. We have just scratched the surface of its functions and features. The list of all possible plots for <GEOM_FUNCTION>() can be found here. You can also make your graphs really “pretty” and professional looking by altering graphing features using <OPTIONS(), including colors, labels, titles and axes. For a list of options that alter various features of a graph, check out Chapter 28 in RDS.

Here’s your ggplot2 badge. Wear it with pride!

Saving plots

You will, on occasion, need to save a plot to a specific file. Specifically, we expect you to create plots and graphs, save them, and upload them for your final project. Don’t use the built-in “Export” button! If you do, your figure is not reproducible – no one will know how your plot was exported. Instead, use ggsave() by explicitly creating the figure and exporting

Let’s save the scatterplot of percent Hispanic and median household income as a .png file named “phisp_inc.png”. First, we save the plot produced by ggplot() into an R object named phisp_inc

phisp_inc <- ggplot(cal.tracts) +
    geom_point(aes(x = phisp, y = medincome)) +
    xlab("Percent Hispanic") +
    ylab("Median Household Income")

Second, make sure you are pointing RStudio into the appropriate folder to save your graph into. Check the working directory using getwd(). We then save phisp_inc using ggsave().

ggsave("phisp_inc.png", phisp_inc)

Navigate to your working directory folder and you should see phisp_inc.png.

Assignment 4

Download and open the Assignment 4 R Markdown Script. Any response requiring a data analysis task must be supported by code you generate to produce your result. Just examining your various objects in the “Environment” section of R Studio is insufficient—you must use scripted commands. Submit the Rmd and its knitted html files on Canvas.

As a comprehensive source for neighborhood data, PolicyMap allows you to examine interesting associations across different dimensions of neighborhood health and well-being outside of those provided in the U.S. Census. Let’s examine the potential predictors of resident health in the City of Sacramento. Bring into R the dataset sac_health_policymap.csv, which contains census-tract level data on Sacramento downloaded from PolicyMap. I’ve also uploaded the file on Canvas (Files - Week 4 - Assignment). Consider the dataset to be cleaned and ready for analysis. A record layout of the data can be found here.

Create an appropriate plot that shows the shape of the distribution for the variable health, which measures the percent of residents reporting very good to excellent health. Describe the shape of the distribution. (2 points)
Examine the association between health and the variable phys. Based on this examination, briefly describe the relationship between the variable health and phys. (2 points)
Create the appropriate plots showing the association between health and the following variables: foodaccess, unemp, and medinc. (3 points)
Based on these plots, briefly describe the relationship between health and the three variables. Describe any nonlinearities in the relationships. (2 points)

The following questions investigate housing structure in Yolo County. Bring into R the dataset ca_border_tracts.csv, which contains 2019-2023 American Community Survey (ACS) data for census tracts in California and states sharing a boundary with California (Arizona, Nevada, and Oregon). I’ve also uploaded the file on Canvas (Files - Week 4 - Assignment). Consider the dataset to be cleaned and ready for analysis. A record layout of the data can be found here.

Calculate 90/10 percentile ratios for median household income for each region (Bay Area, Southern California, Other California, Arizona, Nevada, and Oregon). Present these values in a presentation-ready table using flextable(). Which region exhibits the highest neighborhood income inequality? Lowest? (2 points)
What is the mean, median, interquartile range, and standard deviation of the percentage of houses built after 2000 in Yolo County? Show these values in a presentation-ready table using flextable(). (2 points)
What is the correlation between median household income and percentage of houses built after 2000 in Yolo County? (1 point)
Show a plot investigating any potential outliers in the percentage of houses built after 2000 in Yolo County. (2 points)
Did you find any outliers? If so, how many? What is the mean, median and standard deviation of the percentage of houses built after 2000 in Yolo County without these outliers? What about the correlation between median household income and percentage of houses built after 2000? Present these values in a presentation-ready table using flextable(). (3.5 points)
Comment on what you learned in question 2e. (0.5 points)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Website created and maintained by Noli Brazil